1. POLYHEDRA BASIS DEFINITION
The word polyhedron has slightly different
meanings in geometry and algebraic
geometry.
In geometry, a polyhedron is simply a
three-dimensional solid which consists of a collection of polygons, usually joined
at their edges. In other word, it is a solid in three dimensions with flat faces,
straight edges and sharp corners or vertices.
The word polyhedron comes from the Classical
Greek πολύεδρον, as poly-(stem
of πολύς, "many") + -hedron (form
of ἕδρα, "base" or "seat"). A polyhedron is the
three-dimensional version of the more general polytope (in the geometric sense), which can be
defined in arbitrary dimension. The plural of polyhedron is
"polyhedra" (or sometimes "polyhedrons").
The term "polyhedron" is used
somewhat differently in algebraic
topology, where it is defined as a space that can be built from such
"building blocks" as line segments, triangles, tetrahedra, and their
higher dimensional analogs by "gluing them together" along their
faces. More specifically, it can be defined as the underlying
space of a simplicial
complex (with the
additional constraint sometimes imposed that the complex be finite). In the
usual definition, a polyhedron can be viewed as an intersection of half-spaces,
while a polytope is a bounded polyhedron.
2. Characteristics
2.1 Polyhedral Surface
A
polyhedron’s edge joins 2 faces. Any edge meets 2 vertices, each one at an end.
These characteristics guarantee that the polyhedral surface does not split off
in different direction and is continuously connected.
2.2 Topological Characteristics
The
topological class of a polyhedron is defined by its Euler characteristic and
orientability.
2.2.1 Euler Characteristic
A formula relating the number of polyhedron
vertices V , faces F, and polyhedron edges E of a
simply connected (i.e., genus 0) polyhedron (or polygon). It was
discovered independently by Euler (1752) and Descartes, so it is also known as
the Descartes-Euler polyhedral formula. The formula also holds for some, but
not all, non-convex
polyhedra.
The polyhedral formula states
V – E + F = 2
where:
V is the
number of vertices
E is the
number of edges
F is the
number of faces.
For genus g surfaces,
the formula can be generalized to the Poincaré
formula
X =
V – E + F = X(g),
Where
X(g)
= 2-2 g
,
is the Euler
characteristic, sometimes also known as the Euler-Poincaré
characteristic. The polyhedral formula corresponds to the special case g = 0..
Definition of for a genus surfaces: A
topologically invariant property of a surface defined as the largest number of
nonintersecting simple closed curves that can be drawn on the surface without
separating it. Roughly speaking, it is the number of holes in a surface.
Convex polyhedron
example:
The surfaces of non convex
polyhedra can have various Euler characteristics:
2.2.2 Orientability
A surface is nonorientable if you can walk along some path and
come back to where you started but reflected, as on a Möbius band. In fact a
surface is nonorientable if and only if you can find a Möbius band inside of
it, like in the Klein bottle and the projective plane. A surface is orientable if it's not nonorientable: you can't
get reflected by walking around in it.
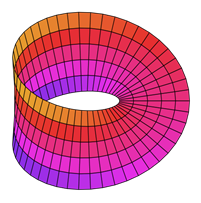 |
| Möbius band |
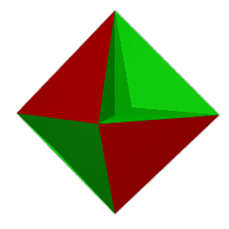 |
tetrahemihexahedron
The tetrahemihexahedron is said to be non-orientable. |
Euler characteristic: Odd-numbered
Euler is a characteristic for non-orientable polyhedrons. For χ < 2, the
polyhedron may or may not be orientable.
2.3 Duality
Duality
is a property of a polyhedron. For every polyhedron there exists a dual polyhedron.
Starting with any regular polyhedron, the dual can be constructed in the following
way :
(1) Place a point in the center of each face of
the original polyhedron;
(2) Connect each new point with the new points
of its neighboring faces;
(3) Erase the original polyhedron.
The dual polyhedron is the polyhedron defined
by the edges drawn in step (2).
It is found that:
• A tetrahedron is dual to a tetrahedron (self
dual);
• A cube
is dual to an octahedron and vice versa;
• A
dodecahedron is dual to an icosahedron and vice versa.
The number of faces in one polyhedron is the
same as the number of vertices in its dual polyhedron since the each vertices
of the dual polyhedron corresponds to a center of the face of the original
polyhedron.
The number of faces in one polyhedron is the
same as the number of vertices in its dual polyhedron since the each vertices
of the dual polyhedron corresponds to a center of the face of the original
polyhedron.
2.4 Vertex
figure
• A face
is a polygon that bounds a polyhedron.
• An edge is a line segment where two faces
meet.
• A vertex is a point at which several edges
and faces meet
• A vertex figure is
the polygon which appears if we truncate a polyhedron at a vertex.
3. Names Of Polyhedra
This table shows that polyhedra are often named
according to the Greek names for their number of faces.
Other polyhedrons, as the pentagonal
dodecahedron, are named according to the kind of faces presented
Some
polyhedra have gained common names, for example the regular hexahedron is
commonly known as the cube.
Others are named after their inventor. For
example, Miller's monster and the Szilassi polyhedron.
Other
names show that some operation has been made on simpler polyhedra, for example
the truncated cube is a cube with its corners cut off.
4. Convex Polyhedra
In
a convex polyhedron, the line segment joining any two vertices of the polyhedron
lies entirely in the interior of the polyhedron. A convex polyhedron has no holes
or indentations.
An
example of a convex polyhedron is illustrated above (Fukuda and Mizukoshi). A
simpler example is the dodecahedron, which is
given by a system with s =12 . Explicit examples
are given in the following table.
In
general, given the matrices, the polyhedron
vertices (and faces) can be found using
an algorithmic procedure known as vertex
enumeration.
Geometrically,
a convex polyhedron can be defined as a polyhedron for which a line connecting any two
(noncoplanar) points on the surface always lies in the interior of the
polyhedron. The 92 convex polyhedra having only regular polygons as faces are called the Johnson solids, which
include thePlatonic
solids and Archimedean
solids. No method is known for computing the volume of a general convex polyhedron
(Grünbaum and Klee 1967, p. 21; Ogilvy 1990, p. 173).
Every
convex polyhedron can be represented in the plane or on the surface of a sphere
by a 3-connected planar graph (called a polyhedral
graph). Conversely, by a theorem of Steinitz as restated by
Grünbaum, every 3-connected planar graph can be realized as a convex polyhedron
(Duijvestijn and Federico 1981). The numbers of vertices V , edges E , and faces F of a convex polyhedron are
related by the polyhedral
formula V + F – E = 2
5. Symmetrical Polyhedral
A
symmetrical polyhedron can be rotated and superimposed on its original position
such that its faces and so on have changed position.
5.1 Regular Polyhedral
A polyhedron is said to be regular if its faces and vertex figures are regular (not necessarily convex) polygons . Using
this definition, there are a total of nine regular polyhedra, five being the convex Platonic solids and four being the concave (stellated) Kepler-Poinsot
solids. However, the term "regular polyhedra" is sometimes
used to refer exclusively to the convex Platonic solids.
It can be proven that only nine regular solids
(in the Coxeter sense) exist by noting that a possible regular polyhedron must
satisfy
 |
The five Platonic solids have an Euler characteristic of 2.
|
 |
the Kepler-Poinsot polyhedra
5.2 Uniform Polyhedra
Uniform
Polyhedra are polyhedra with the following properties:
- all faces are regular polygons
(which may include star polygons like pentagrams)
- all vertices are equivalent
A
few special cases:
- the five regular or Platonic
solids (all faces identical convex polygons)
- the thirteen semi-regular or
Archimedean solids (all faces convex polygons, but not all identical)
- the four Kepler-Poinsot solids
(non-convex, but all faces identical polygons)
- an infinite number of prisms
and antiprisms
Excluding
the prisms, there are 76 uniform polyhedra.
Some
example of uniform polyhedral:
5.3 Pyramids
A polyhedron is a pyramid if it has 3 or more triangular faces sharing a common vertex.
A pyramid is a polyhedron that has only one base. The base of a pyramid may be any polygon. If we restrict ourselves to regular polygons
for faces, there are three possible pyramids: the triangle-based tetrahedron (It has four faces. It is the simplest polyhedron, called
a tetrahedron from the Greek word "tetra", meaning "four"),
the square pyramid, and
the pentagonal pyramid. Being bounded by regular polygons, these last
two fall within the class of Johnson solids. One
interesting property of pyramids is that like the tetrahedron, their duals are also
pyramids.
The regular pentagonal pyramid having equilateral triangles as
faces so that all its edges are of the same length is Johnson solid
5.4 Noble
Polyhedra
A noble polyhedron’s faces are all the same and all its vertices are also all the same. They were studied mainly by Hess, Bruckner and later
by Grünbaum.
The dual of a noble
polyhedron is also noble. Many of them are
self-dual.
5. Polyhedra with Regular Faces
A polyhedron is said to be regular if all its faces are equal regular
polygons and the same number of faces meet at every vertex. A polyhedron formed
by the {p} polygons with q meeting at every vertex is denoted {p, q}.
Convex polyhedra where every face is
the same kind of regular polygon may be found among three families such as
triangles, squares and pentagons.
5.2 Johnson
Solid
Let’s see the definition of Archimedean
polyhedral; Archimedean polyhedra are convex uniform polyhedra, of which
there are thirteen. The Archimedean polyhedra are polyhedra with regular
polygon faces. Faces may be of different types but all the vertices are
identical. Except for the truncated tetrahedron, all the Archimedean
polyhedra are modifications of the cube-octahedron pair or the dodecahedron-icosahedron
pair.]
As in any strictly convex solid, at least three
faces meet at every vertex, and the total of their angles is less than 360
degrees. Since a regular polygon has angles at least 60 degrees, it follows
that at most five faces meet at any vertex. The pentagonal pyramid (J2) is an example
that actually has a degree-5 vertex.
Although there is no obvious restriction that
any given regular polygon cannot be a face of a Johnson solid, it turns out
that the faces of Johnson solids always have 3, 4, 5, 6, 8, or 10 sides.
In 1966, Norman Johnson published a list which included all 92
solids, and gave them their names and numbers. He did not prove that there were
only 92, but he did conjecture that there were no others. Victor
Zalgaller in 1969
proved that Johnson's list was complete.
Of the Johnson solids, the elongated square gyrobicupola (Fig 13), also called the
pseudorhombicuboctahedron, is
unique in being locally vertex-uniform: there are 4 faces at each vertex, and
their arrangement is always the same: 3 squares and 1 triangle. However, it is
not vertex-transitive, as it has different isometry at different vertices,
making it a Johnson solid rather than an Archimedean
solid.
7. Defining a cube using MATLAB Graphics
A cube
is defined by eight vertices that form six sides. This illustration shows the
coordinates of the vertices defining a cube in which the sides are one unit in
length:
|
Specifying X, Y,
and Z Coordinates
Each of the six faces has four vertices. Since you do not
need to close each polygon (i.e., the first and last vertices do not need to be
the same), you can define this cube using a 4-by-6 matrix for each of the x-,y-, and z-coordinates.
Each column of the matrices specifies a different face. Note
that while there are only eight vertices, you must specify 24 vertices to
define all six faces. Since each face shares vertices with four other faces,
you can define the patch more efficiently by defining each vertex only once and
then specifying the order in which to connect these vertices to form each face.
The patch Vertices and Faces properties define patches in just this
way.
Specifying Faces and Vertices
These matrices specify the cube using Vertices and Faces:
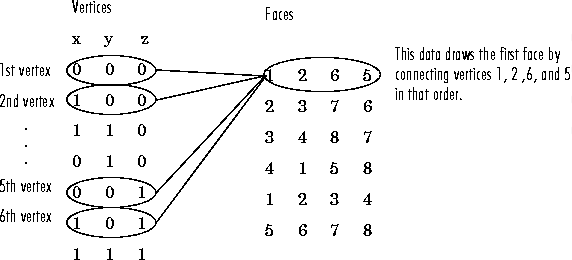
Using
the vertices/faces technique can save a considerable amount of computer memory
when patches contain a large number of faces. This technique requires the
formal patch function syntax, which entails
assigning values to the Vertices and Faces properties explicitly. For example,
patch('Vertices',vertex_matrix,'Faces',faces_matrix)
Since the formal syntax does not automatically assign face or
edge colors, you must set the appropriate properties to produce patches with
colors other than the default white face color and black edge color.
Flat Face Color
Flat face color is the result of specifying one color per
face. For example, using the vertices/faces technique and the FaceVertexCData property to define color, this
statement specifies one color per face and sets the FaceColor property to flat.
patch('Vertices',vertex_matrix,'Faces',faces_matrix,...
'FaceVertexCData',hsv(6),'FaceColor','flat')
Since true color specified with the FaceVertexCData property has the same format as a
MATLAB colormap (i.e., an n-by-3 array of RGB values), this
example uses the hsv colormap to generate the six colors
required for flat shading.
Interpolated Face
Color
Interpolated face color means the vertex colors of each face
define a transition of color from one vertex to the next. To interpolate the
colors between vertices, you must specify a color for each vertex and set the FaceColor property to interp.
patch('Vertices',vertex_matrix,'Faces',faces_matrix,...
'FaceVertexCData',hsv(8),'FaceColor','interp')
Changing to the standard 3-D view and making the axis square,
view(3); axis square
produces a cube with each face colored by interpolating the
vertex colors.
To
specify the same coloring using the x, y, z, c technique, c must be an m-by-n-by-3 array, where the dimensions of
x, y, and z are m-by-n.
This diagram shows the correspondence between the FaceVertexCData and CData properties\
.
Specifying Patch Coloring
Patch objects employ a coloring scheme that is basically
different from that used by surface objects in that patches do not
automatically generate color data based on the value of the z-coordinate
at each vertex. You must explicitly specify patch coloring, or MATLAB uses the
default white face color and black edge color.
Patch coloring methods provide a means to display pictures of
real-world objects with information superimposed on them through the use of
color. For example a picture of an airplane wing can be colored to indicate the
air pressure across its surface.
This table summarizes the patch properties that control color
(exclusive of those used when light sources are present). See patch properties for a complete list of properties.
8. Polyhedral In Real Life











































